Preparing for Q-Day

Linda Ikechukwu

Follow Smallstep

With new US Congress legislation mandating agencies to adopt quantum-resistant cryptography, the race to secure data against future quantum threats is on.

In response, we’ve updated both our open-source and commercial products to support X25519MLKEM768, a post-quantum TLS 1.3 Hybrid Key Exchange that merges X25519 (a classic elliptic curve cryptography algorithm) and ML-KEM-768 (a post-quantum key encapsulation mechanism standardized in FIPS 203 under NIST’s post-quantum cryptography efforts).

This TLS hybrid key exchange approach defends your data from classical threats today and potential quantum attacks tomorrow (otherwise called “harvest now, decrypt later” attacks). In a hybrid key exchange, the client and server each generate partial secrets with both algorithms, then combine them into one shared session key. If a quantum computer eventually cracks X25519, Kyber768 still keeps your session secure, and vice versa.

What’s “harvest now, decrypt later”? What is quantum computing? And why does any of this matter? I try to answer all those questions in this article.

The quantum computing threat

The origins of quantum computing can be traced back to physicist Richard Feynman’s seminal 1981 talk, “Simulating Physics with Computers”. Feynman believed that if you wanted to efficiently simulate and deeply understand quantum phenomena (such as chemical reactions, material behavior, or particle physics), you had to build a computer that operated on quantum principles.

Feynman also believed that a computer that could naturally model complex quantum phenomena would enable groundbreaking advances in medicine, material science, fundamental physics research, and so much more. Classical computers (our everyday computers) struggle to do these tasks effectively because they rely on transistors and binary bits to process and store information. As expected, Feynman’s idea sparked curiosity.

Today, the quest for quantum computers is driven by more than theoretical curiosity. As advancements in artificial intelligence and machine learning continue, researchers demand more computational power, pushing classical computing hardware to its physical limits.

We’ve gone from Intel’s 4004 10,000 nm, released in 1971, to Apple’s M4 Ultra 3nm and soon to TSMC’s 2nm node, expected sometime in 2025. As transistors approach below 1 nm shrinkage, they reach atomic scales where electron tunneling causes leakage currents, degrading performance and reliability. This inevitable terminus poses a clear need for alternative computing architectures, such as quantum computing, to overcome these fundamental limitations.

Unlike classical computers, quantum computers rely on physical quantum mediums (like superconducting circuits, trapped ions, and photons) instead of binary transistors. Information in quantum computers is stored using quantum bits (qubits), which also have two basic states: 0 and 1. However, while binary bits can only be in a state of either 0 or 1, qubits can exist in an arbitrary combination of both states and everything in between; a condition known as superposition.

This superposition property allows quantum computers to perform calculations like cracking cryptographic encryption schemes exponentially faster (in a matter of days).

Tech giants like IBM and Google have successfully built quantum processors with over 100 qubits. In theory, these processors can process more information than classical supercomputers with billions of transistors. Although impressive, millions of stable, fault-tolerant qubits are needed for a quantum computer to break current cryptography schemes. While this is not yet a reality, it is an imminent possibility. This is why governments, researchers, and scientists have been exploring new ways to encrypt data that can withstand attacks from both normal and quantum computers (dubbed post-quantum cryptography).

Right now, nation-states and malicious actors are likely intercepting valuable encrypted data—such as medical research, top-secret intelligence, or sensitive personal information—and storing it in anticipation of Q-day (the day quantum computers will be advanced enough to break current encryption schemes). This tactic is known as the "harvest now, decrypt later" attack vector.

Why quantum computers will be able to break current encryption mechanisms.

Public key cryptography frameworks like RSA and ECC make securely exchanging information over insecure channels with unknown entities possible, with two key provisions:

• Authentication: Digital signature algorithms (e.g., RSA, ECDSA, EdDSA) are used in X.509 certificates or software packages to verify identity and ensure authenticity.
• Encryption key exchange: Algorithms like RSA and ECDH allow a browser and server to securely exchange a secret session key, enabling encrypted communication.

The problem? None of these are quantum-resistant.

Current public key cryptographic algorithms are built on mathematically tricky problems, like factoring large prime numbers or solving discrete logarithms, which require an exponential amount of time to solve. As the key sizes increase, the time needed to break (or rather guess) these keys grows exponentially. Since classical computers struggle with exponential time complexity, we have remained safe.

Take RSA, for example, which derives its security from the mathematical difficulty of factoring large numbers. It selects two large prime numbers (let’s call them p and q) at random and multiplies them to generate the public key. The private key is then derived using the totient function of p and q, defined as:

ϕ(N) = (p - 1) × (q - 1)

If an attacker knows p and q, they can break RSA. Multiplying two primes is easy, but reversing that process (prime factorization) grows exponentially harder as N becomes larger. The number of possible factors and the time needed to check them explodes.

Let me break it down.

When you multiply two prime numbers, the result is always a composite number that has exactly four factors:

1. 1 (since every number is divisible by 1)
2. p (the first prime number)
3. q (the second prime number)
4. N (the product of the two primes, i.e., N = p \times q )

See below the increasing difficulty of finding the prime factors of the product of two prime numbers, starting with the smallest primes (excluding 1): 3 and 5.

Now imagine trying to find the prime factors of a 2048 bit RSA key (~617 decimal digits), which is the current minimum security standard for RSA encryption. To factor such a number by trial, you’d need to check approximately  10^{308}  possible prime factors.

For perspective, a number that far exceeds:

• The number of atoms in the observable universe (~ 10^{80} ).
• The estimated number of grains of sand on Earth (~ 10^{23} ).
• The number of seconds since the Big Bang (~ 10^{17} ).

As I mentioned, in regular classical computers, each bit is either 0 or 1. A quantum computer, however, uses qubits, which can hold any combination of 0 and 1 at the same time, a phenomenon called superposition.

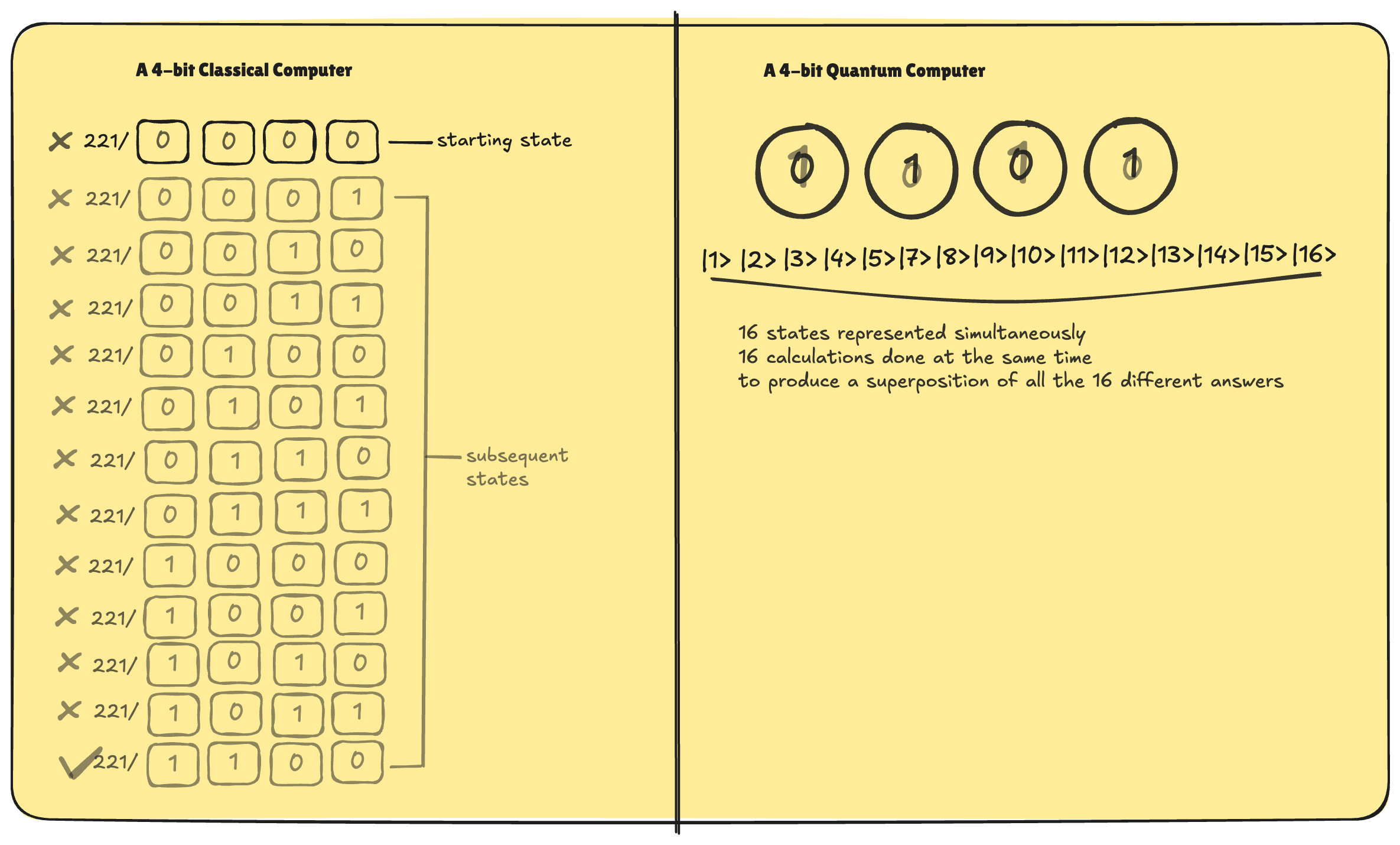
With four bits classical computer, you can represent 16 possible states (from 0000 to 1111, corresponding to the numbers 0 through 15). But the computer can only be in one of those states at any given moment. If you tried to use such a computer to find the prime factors of 221, it would test prime candidates in sequence, starting with 3, then 5, then 7, until it finds that 221 divides evenly by 13, giving 17.

In contrast, with four qubits, a quantum computer (using something like Shor’s Algorithm) can hold all 16 possible states (from 0000 to 1111) simultaneously, effectively doing 16 calculations at once. If you increase the number of qubits to 20, you can represent over a million different states, meaning you can compute over a million different outcomes at the same time. With 300 qubits, the number of possible states exceeds the number of particles in the observable universe. These figures hint at the extraordinary potential of quantum computing.

After performing all the calculations simultaneously to arrive at a superposition of all possible answers, quantum computers use another quantum mechanics property known as entanglement to pinpoint, or measure, the correct answer from the bunch. (To avoid this article being longer than it should, I will not delve into the details of entanglement here, but the resources below offer a deeper explanation)

In summary, thanks to superposition and entanglement, a quantum computer can theoretically accomplish tasks in days that might take a classical computer years.

Supercomputers use parallelization effectively for tasks like machine learning, because those workloads can be sliced into largely independent chunks. Prime factoring, on the other hand, is different. It demands continuous coordination among processors to see if each tested factor works, which slows everything down. Even a high-end supercomputer such as Fugaku, which can perform about 10^18 operations per second, would still need millions of years to brute-force a 2,048-bit RSA key.

How post-quantum cryptography algorithms work

In 2016, the US National Institute of Standards and Technology (NIST) invited researchers worldwide to submit quantum-safe or quantum-resistant algorithms. After multiple rounds of rigorous assessment, NIST announced its recommended post-quantum cryptographic standards in August 2024 (FIPS 203, 204, and 205):

• ML-KEM (Module-Lattice-Based Key Encapsulation Mechanism) relies on CRYSTALS-Kyber for general encryption. It replaces traditional public-key encryption and key exchange algorithms like RSA Key Exchange, ECDH, and Diffie-Hellman.
• ML-DSA (Module-Lattice-Based Digital Signature Algorithm) is built on CRYSTALS-Dilithium for digital signatures, providing authenticity and integrity of messages. It replaces existing signature schemes used in TLS certificates, code signing, blockchain transactions, and more.
• SLH-DSA serves as a backup if ML-DSA is found to be vulnerable.

What these algorithms have in common is that they’re based on the mathematics of lattices, a complex mathematical structure believed to be difficult for quantum computers to solve.

A lattice is like a grid created by combining two or more vectors repeatedly. Picture a sheet of graph paper with two vectors, r1 and r2. If you combine integer multiples of these vectors (like three steps in the r1 direction and one step in the r2 direction), you’ll land on certain points. All the points you can reach by combing the integer multiples of r1 and r2 together form what’s called a lattice, much like the way atoms or molecules arranged within a crystalline solid.

Now imagine a target point C on that same graph paper. If you know the original vectors r1 and r2, it is straightforward to figure out which combination of the two gets you close to C. However, the same lattice can also be generated by “bad vectors” such as b1 and b2 below, which are not so intuitive. With these bad vectors, finding the closest point to C isn’t as straightforward anymore. This dilemma is called the closest vector problem, and it is the foundation of lattice-based cryptography.

The idea is that this closest vector problem becomes extremely difficult as the number of dimensions grows. While it’s relatively simple in two or three dimensions, once you reach hundreds or thousands, it becomes practically impossible, even for quantum computers.

So how do we use this to encrypt data?

Each user in a lattice-based encryption scheme has two sets of vectors:

• A private set (the “ original or good” vectors), which are straightforward to use.
• A public set (the “bad” vectors), which is deliberately made hard.

If I want to send someone a secret message, I pick a point on their lattice to represent the message, then add some random noise. This shifts the point slightly away from its “true” location. To decode that noisy point, the recipient needs to figure out which exact lattice point it corresponds to. Without the private (good) vectors, that’s nearly impossible. But for the intended recipient, who holds the private vectors, it’s simple.

As dimensions go up, the complexity of this problem skyrockets. Unlike a two-dimensional grid, the lattices used in cryptography can span hundreds or thousands of dimensions. Even if you find a lattice point that seems close to your target, you’d still have to check an enormous number of other points to confirm it’s the absolute closest.

Today, the closest vector problem is so complex that neither classical nor quantum computers can feasibly solve it in high dimensions. The only feasible way to decrypt the data is if you hold the simplified (or “reduced”) set of vectors, which is the private key.

The best time to start thinking quantum-safe is now.

Supporting hybrid TLS handshakes is the first step in migrating to quantum-safe TLS connections, and we’ve done that.

With the latest releases of step-ca (our open source certificate authority, > v0.28.3) and step-cli (our open source PKI CLI tool, > v0.28.6), you can use a TLS 1.3 hybrid key exchange with X25519Kyber768 / ML-KEM. However, it’s not enabled by default, so you’ll need to set GODEBUG=tlsmlkem=1 until we update go.mod to 1.24 (planned for August 2025, when Go 1.25 becomes available). If you use another TLS client, it must also support X25519MLKEM768; otherwise, the connection falls back to a traditional key exchange.

The next goal for the ecosystem is to adopt hybrid X.509 certificates and a hybrid CA, which include both a classical (pre-quantum) key pair and a post-quantum (PQ) key pair. This ensures compatibility with existing systems while gradually introducing PQ algorithms. After that, we need to update relevant software and infrastructure so they recognize and use the PQ keys within these hybrid certificates, making interoperability easier during the transition. Finally, once every system fully supports post-quantum algorithms, we can remove the pre-quantum key pair and start issuing smaller PQ-only certificates.

At the moment, these follow-up steps are stalled because ML-DSA signatures and their public keys remain too large and slow for practical use. That’s why no major browser or client is deploying post-quantum signatures yet. We’ve taken the first step by incorporating a hybrid TLS handshake, and we plan to add more updates once NIST introduces smaller, faster signatures through its follow-up competition.

On a related note, if you rely on AD CS, it is unlikely Microsoft will add post-quantum support to AD CS. Organizations using AD CS should explore alternatives now so they are better positioned to migrate to PQC. Maybe you should be talking to us 🙂.

References/More Reading

• TLS 1.3 Hybrid Key Exchange using ML-KEM
• NIST Module-Lattice-Based Key-Encapsulation Mechanism Standard
• Post-Quantum Cryptography Is Too Damn Big.